STAM101 :: Lecture 11 :: Attributes

Contingency table – 2x2 contingency table – Test for independence of attributes – test for goodness of fit of mendalian ratio

Test based on  -distribution

In case of attributes we can not employ the parametric tests such as F and t. Instead we have to apply test. When we want to test whether a set of observed values are in agreement with those expected on the basis of some theories or hypothesis. The statistic provides a measure of agreement between such observed and expected frequencies.

Chi-Square

The  test has a number of applications. It is used to

• Test the independence of attributes
• Test the goodness of fit
• Test the homogeneity of variances
• Test the homogeneity of correlation coefficients
• Test the equaslity of several proportions.

In genetics it is applied to detect linkage.

Applications

– test for goodness of fit

A very powerful test for testing the significance of the discrepancy between theory and experiment was given by Prof. Karl Pearson in 1900 and is known as “chi-square test of goodness of fit “.

If 0i, (i=1,2,…..,n) is a set of observed (experimental frequencies) and Ei (i=1,2,…..,n) is the corresponding set of expected (theoretical or hypothetical) frequencies, then,
 
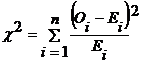
It follows a  distribution with n-1 d.f.  In case of only one tailed test is used.

 

 

Example

            In plant genetics, our interest may be to test whether the observed segregation ratios deviate significantly from the mendelian ratios. In such situations we want to test the agreement between the observed and theoretical frequency, such test is called as test of goodness of fit.

Conditions for the validity of -test:
-test is an approximate test for large values of ‘n’ for the validity of -test of goodness of fit between theory and experiment, the following conditions must be satisfied.

• The sample observations should be independent.

 

2. Constraints on the cell freqrequency, if any, should be linear.    
Example:=.

3. N, the total frequency should be reasonably large, say greater then (>) 50.

4. No theoretical cell frequency should be less than (<)5. If any theoretical cell frequency is <5, then for the application of - test, it is pooled with the  preceding or scecceeding frequency so that the pooled frequency is more  than 5 and finally adjust for degree’s of freedom lost in pooling.

Example1
The number of yiest cells counted in a haemocytometer is compared to the theoretical value is given below. Does the experimental result support the theory?

 

Solution
H0: the experimental results support the theory
H1: the esperimental results does not support the theory.
Level of significance=5%
Test Statistic:
 

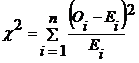
Oi	Ei	Oi­-Ei	(Oi­-Ei)2	(Oi­-Ei)2/Ei
103	106	-3	9	0.0849
143	141	2	4	0.0284
98	93	5	25	0.2688
42	41	1	1	0.0244
8	14	-6	36	2.5714
6	5	1	1	0.2000
400	400			3.1779

\=3.1779

Table value
(6-1=5 at 5 % l.os)= 11.070
Inference
<tab
We accept the null hypothesis.
(i.e) there is a good correspondence between theory and experiment.

test for independence of attributes

            At times we may consider two charactertistics on attributes simultaneously. Our interest will be to test the association between these two attributes
Example:- An entomologist may be interested to know the effectiveness of different concentrations of the chemical in killing the insects. The concentrations of chemical form one attribute. The state of insects ‘killed & not killed’ forms another attribute. The result of this experiment can be arranged in the form of a contingency table.  In general one attribute may be divided into m classes as A 1,A 2, …….A m  and the other attribute may be divided into  n classes as B 1,B 2, ……B n . Then the contingency table will have m x n cells. It is termed as m x n contingency table

where Oij’s are observed frequencies.
The expected frequencies corresponding to Oij is calculated as . The is computed as
    
where
Oij – observed frequencies
Eij – Expected frequencies
n= number of rows
m= number of columns
It can be verified that
This  is distributed as  with (n-1) (m-1) d.f.

2x2 – contingency table

            When the number of rows and numberof columns are equal to 2 it is termed as 2 x 2 contingency table .It will be in the following form

Where a, b, c and d are cell frequancies c1 and c2 are column totals, r1 and r2 are row totals and n is the total number of observations.
In case of 2 x 2 contigency table  can be directly found using the short cut formula,
   
The d.f  associated with is (2-1) (2-1) =1

Yates correction for continuity
If anyone of the cell frequency is < 5, we use Yates correction to make as continuous. The yares correction is made by adding 0.5 to the least cell frequency and adjusting the other cell frequencies so that the column and row totals remain same . suppose, the firat cell frequency is to be corrected then the consigency table will be as follows:

Then  use the - statistic as

               
The d.f  associated with is (2-1) (2-1) =1

Exapmle 2
The severity of a disease and blood group were studied in a research projest. The findings sre given in the following table, knowmn as the m xn contingency table. Can this severity of the condition and blood group are associated.
Severity of a disease classified by blood group in 1500 patients.

Condition	Blood Groups				Total
	O	A	B	AB
Severe	51	40	10	9	110
Moderate	105	103	25	17	250
Mild	384	527	125	104	1140
Total	540	670	160	130	1500

Solution
H0: The severity of the disease is not associated with blood group.
H1: The severity of the disease is associated with blood group.
Calculation of Expected frequencies

Condition	Blood Groups				Total
	O	A	B	AB
Severe	39.6	49.1	11.7	9.5	110
Moderate	90.0	111.7	26.7	21.7	250
Mild	410.4	509.2	121.6	98.8	1140
Total	540	670	160	130	1500

Test statistic:
  
The d.f. associated with the   is (3-1)(4-1) = 6
Calculations

Oi	Ei	Oi­-Ei	(Oi­-Ei)2	(Oi­-Ei)2/Ei
51	39.6	11.4	129.96	3.2818
40	49.1	-9.1	82.81	1.6866
10	11.7	-1.7	2.89	0.2470
9	9.5	-0.5	0.25	0.0263
105	90.0	15	225.00	2.5000
103	111.7	-8.7	75.69	0.6776
25	26.7	-1.7	2.89	0.1082
17	21.7	-4.7	22.09	1.0180
384	410.4	-26.4	696.96	1.6982
527	509.2	17.8	316.84	0.6222
125	121.6	3.4	11.56	0.0951
104	98.8	5.2	27.04	0.2737
Total				12.2347

\=12.2347
Table value of for 6 d.f. at 5% level of significance is 12.59
Inference
<tab
We accept the null hypothesis.
The severity of the disease has no association with blood group.

Example 3
In order to determine the possible effect of a chemical treatment on the rate of germination of cotton seeds a pot culture experiment was conducted. The results are given below
Chemical treatment and germination of cotton seeds

	Germinated	Not germinated	Total
Chemically Treated	118	22	140
Untreated	120	40	160
Total	238	62	300

Does the chemical treatrment improve the germination rate of cotton seeds?

Solution
H0:The chemical treatment does not improve the germination rate of cotton seeds.
H1: The chemical treatment improves the germination rate of cotton seeds.
Level of significance = 1%
Test statistic
  
 

 

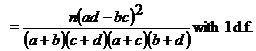
Table value
(1) d.f. at 1 % L.O.S = 6.635
Inference
 <tab
We accept the null hypothesis.
The chemical treatmentwill not  improve the germination rate of cotton seeds significantly.

Example 4
In an experiment on the effect of a growth regulator on fruit setting in muskmelon the following results were obtained. Test whether the fruit setting in muskmelon and the application of growth regulator are independent at 1% level.

	Fruit set	Fruit not set	Total
Treated	16	9	25
Control	4	21	25
Total	20	30	50

Solution
H0:Fruit setting in muskmelon does not depend on the application of growth regulator.
H1: Fruit setting in muskmelon depend on the application of growth regulator.
Level of significance = 1%
After Yates correction we have 

	Fruit set	Fruit not set	Total
Treated	15.5	9.5	25
Control	4.5	20.5	25
Total	20	30	50

 

Tet statistic
    
 

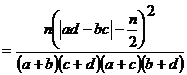
Table value
(1) d.f. at 1 % level of significance is 6.635
Inference
 >tab
We reject the null hypothesis.
Fruit setting in muskmelon is influenced by the  growth regulator. Application of growth regulator will increase fruit setting in musk melon.

Download this lecture as PDF here