MATHS :: Lecture 23 :: Vectoralgebra

 Vector Algebra
A quantity having both magnitude and direction is called a vector.
Example: velocity, acceleration, momentum, force, weight etc.

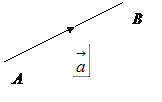
Vectors are represented by directed line segments such that the length of the line segment is the magnitude of the vector and the direction of arrow marked at one end denotes the direction of the vector.

 A vector denoted by =  is determined by two points A, B such that the magnitude of the vector is the length of the line segment AB and its direction is that from A to B. The point A is called initial point of the vector and B is called the terminal point. Vectors are generally denoted by (read as vector a, vector b, vector c,…)
Scalar
A quantity having only magnitude is called a scalar.
Example: mass, volume, distance  etc.
Addition of vectors
If  and   are two vectors, then the addition of  from  is denoted by  +   
This is known as the triangle law of addition of vectors which states that, if two vectors are represented in magnitude and direction by the two sides of a triangle taken in the same order, then their sum is represented by the third side taken in the reverse order.
 

 

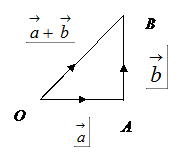
Subtraction of Vectors
            If  and   are two vectors, then the subtraction of  from  is defined as the vector sum of  and -  and is denoted by  -   
                              -   = +(-   )                                   
Types of Vectors
Zero or Null or a Void Vector
A vector whose initial and terminal points are coincident is called zero or null or a void vector. The zero vector is denoted by .
Proper vectors 
Vectors other than the null vector are called proper vectors.

Unit Vector

A vector whose modulus is unity, is called a unit vector.
The unit vector in the direction of  is denoted by . Thus .
There are three important unit vectors, which are commonly used, and these are the vectors in the direction of the x, y and z-axes. The unit vector in the direction of the x-axis is, the unit vector in the direction of the y-axis is  and the unit vector in the direction of the z-axis is .
 Collinear or Parallel vectors
Vectors are said to be collinear or parallel if they have the same line of action or have the lines of action parallel to one another.
Coplanar vectors
Vectors are said to be coplanar if they are parallel to the same plane or they lie in the same plane.
Product of Two Vectors
There are two types of products defined between two vectors.
They are (i) Scalar product or dot product
(ii) Vector product or cross product.

Scalar Product (Dot Product)
The scalar product of two vectors  and   is defined as the number, where  is the angle between  and . It is denoted by . .
Properties

1. Two non-zero vectors 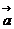 and 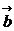 are perpendicular if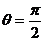

    \  . = 0

2. Let  be three unit vectors along three mutually perpendicular directions. Then by definition of dot product,   and
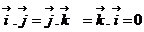
3. If m is any scalar, ==
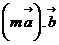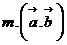
4. Scalar product of two vectors in terms of components

                  Let  : .
Then
=   +  +                  

=   a1b1 + a2b2 + a3b3                            

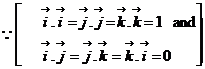
5. Angle between the two vectors

                             . =

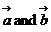
Work done by a force:
Work is measured as the product of the force and the displacement of its point of application in the direction of the force.
Let  represent a force and  the displacement of its point of application and  is angle between and.

.   =                                                  
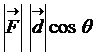
Vector Product (Cross Product)
The vector product of two vectors  and is defined as a vector  sin , where  is the angle from  and , is the unit vector perpendicular to such that  form a right handed system.  It is denoted by .  (Read: )    

       
                                                                                    A                                                       
                                                                
                                                                     
                                                                       
                                                                                                                                                           
                          B                  
Properties
1. Vector product is not commutative

=                                    
2. Unit vector perpendicular to
                                                                             ………(i)
                                                            ………(ii)
            (i) ¸ (ii) gives =
3. If two non-zero vectors  are collinear then
           
Note
If then        (i) =, is any non-zero vector or
                                    (ii) =,is any non-zero or
                             (iii)  and are collinear or parallel.
4. Let be three unit vectors, along three mutually perpendicular directions. Then by definition of vector product

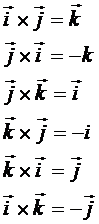
5. (m) x = x (m) = m(x )where m is any scalar.
6. Geometrical Meaning of the vector product of the two vectors is the area of the parallelogram whose adjacent sides are and               

Note
Area of triangle with adjacent sides = x )
7. Vector product in the form of a determinant
Let =
Then =( ) x ()
=
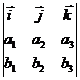
8. The angle between the vectors

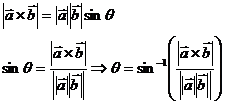
Moment of Force about a point
The moment of a force is the vector product of the displacement and the force
(i.e) Moment

Download this lecture as PDF here