MATHS :: Lecture 21 :: Solving simulteneous equation and cramers rule

 
INVERSE OF A MATRIX
Definition

Let A be any square matrix.  If there exists another square matrix B Such that AB = BA = I (I is a unit matrix) then B is called the inverse of the matrix A and is denoted by A-1.
The cofactor method is used to find the inverse of a matrix. Using matrices, the solutions of simultaneous equations are found.

Introduction to Vectors

Vector Transformations

Vector Dot Product and Vector Length

Unit Vectors

Matrix Vector Products

Matrices to solve a vector combination problem

Converting a line from Cartesian to vector form

Working Rule to find the inverse of the matrix
Step 1: Find the determinant of the matrix.
Step 2: If the value of the determinant is non zero proceed to find the inverse of the matrix.
Step 3: Find the cofactor of each element and form the cofactor matrix.
Step 4: The transpose of the cofactor matrix is the adjoint matrix.
Step 5:  The inverse of the matrix A-1 =
Example
Find the inverse of the matrix
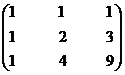
Solution
Let A =
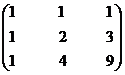
Step 1

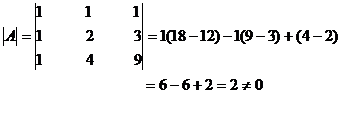
Step 2
The value of the determinant is non zero
\A-1 exists.
Step 3
Let Aij denote the cofactor of aij in









Step 4
The matrix formed by cofactors of element of determinant  is
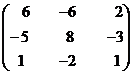
\adj A =
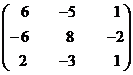
Step 5

=                  

 

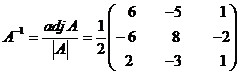
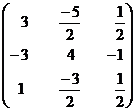
Download this lecture as PDF here