MATHS :: Lecture 03 :: Bionomial

BINOMIAL THEOREM
A Binomial is an algebraic expression of two terms which are connected by the operation  ‘+’ (or) ‘-‘
For example,  x+siny, 3x2+2x, cosx+sin x etc… are binomials.
Binomial Theorem for positive integer:
If n is a positive integer then

----(1)

Some Expansions
a) If we put a = -a in the place of   a in

b) Put  x =1 and a = x in (1)
   
     ----------(2)
c) Put  x = 1 and  a = -x in (1)
  
-----------(3)
(d) Replacing n by – n in equation (2)
 ---------(4)
e) Replacing n by – n in equation (3)
 -----------(5)
Special Cases
1.
2. 
3.
4.
Note:
1. There are n+1 terms in the expansion of (x+a)n.
2. In the expansion the general term is . Since this is the (r+1)th term, it is denoted by Tr+1 i.e. .
3.  are called binomial coefficients.
4. From the relation, we see that the coefficients of terms equidistant from the beginning and the end are equal.
Note:  The  number of terms in the expansion of (x+a)n depends upon the index n. the index is  either even (or) odd. Then the middle term is
Case(i): n is even
The number of terms in the expansion is (n+1), which is odd.
Therefore, there is only one middle term and is given by
Case(ii) : n is odd
The number of terms in the expansion is (n+1), which is even.
Therefore, there are two middle terms and they are given by   and   
Examples
1. Expand   (i)   
2. Find 117.
Solution:
117=  (1+10)7


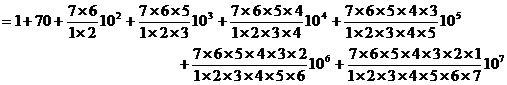
= 1+ 70 + 2100 +35000 + 350000 + 2100000 + 7000000 + 10000000
= 19487171

2. Find the coefficient of x5 in the expansion of
Solution
In the expansion of, the general term is


Let  be the term containing x5
then, 17-4r = 5 Þ r = 3
\  =
= 680 x5
\coefficient of x5 = 680.
3. Find the constant term in the expansion of 
Solution
In the expansion of, the general term is



Let  be the Constant term then,
= 0Þ r = 2
\ The constant term           
=    = 180

 

Download this lecture as PDF here