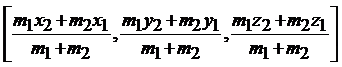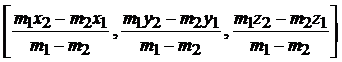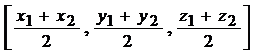MATHS :: Lecture 01 :: 3D Analytical Geometry

Three dimensional Analytical geometry
Let OX ,OY & OZ be mutually perpendicular straight lines meeting at a point O. The extension of these lines OX1, OY1 and OZ1  divide the space at O into octants(eight).  Here mutually perpendicular lines are called X, Y and Z co-ordinates axes and O is the origin. The point P (x, y, z) lies in space where x, y and z are called x, y and z coordinates respectively

.

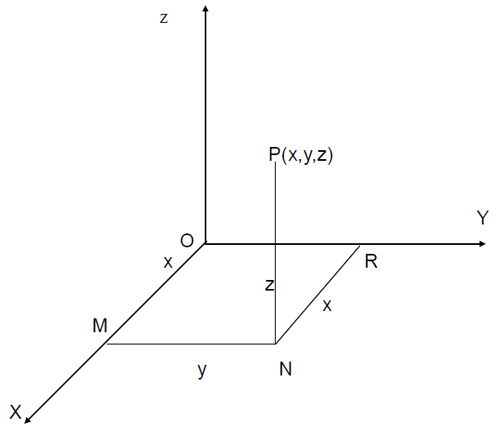
where NR = x coordinate, MN = y coordinate and PN = z coordinate

Distance between two points

The distance between two points A(x1,y1,z1) and B(x2,y2,z2) is

   dist AB =

In particular the distance between the origin O (0,0,0) and a point P(x,y,z) is

               OP =
The internal and External section
Suppose P(x1,y1,z1) and Q(x2,y2,z2) are two points in three dimensions.

 

P(x1,y1,z1)                                 A(x, y, z)                                            Q(x2,y2,z2)
The point A(x, y, z) that divides distance PQ internally in the ratio m1:m2 is given by

 

A =

 

Similarly
P(x1,y1,z1) and Q(x2,y2,z2) are two points in three dimensions.

 

                     P(x1,y1,z1)                                  Q(x2,y2,z2)                                  A(x, y, z)
The point A(x, y, z) that divides distance PQ externally in the ratio m1:m2 is given by

 

A =

 

If A(x, y, z)  is the midpoint then the ratio is 1:1

A =

 

Problem
Find the distance between the points P(1,2-1) & Q(3,2,1)
PQ= ===2
Direction Cosines

     Let P(x, y, z) be any point and OP = r. Let a,b,g  be the angle made by line OP with OX, OY & OZ. Then a,b,g are called the direction angles of the line OP. cos a, cos b, cos g  are called the direction cosines (or dc’s) of the line OP and are denoted by the symbols I, m ,n

.Result
By projecting OP on OY, PM is perpendicular to y axis and the  also OM = y
               
Similarly,   
                 
(i.e)  l =  m =  n =
            \l2 + m2 + n2 =
(Distance from the origin)
\ l2 + m2 + n2 =     
    l2 + m2 + n2 = 1
(or)      cos2a + cos2b + cos2g = 1.
Note :-
            The direction cosines of the x axis are (1,0,0)
            The direction cosines of the y axis are (0,1,0)
           The direction cosines of the z axis are (0,0,1)
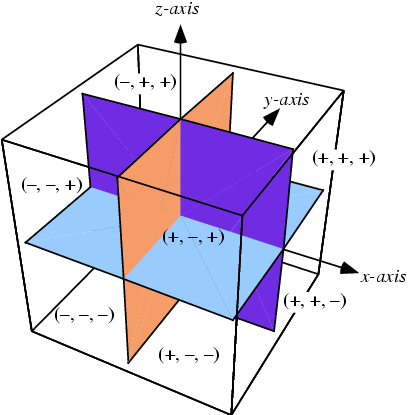
Direction ratios
            Any quantities, which are proportional to the direction cosines of a line, are called direction ratios of that line.  Direction ratios are denoted by a, b, c.
            If l, m, n are direction cosines an a, b, c are direction ratios then
            a µ l, b µ m, c µ n
            (ie) a = kl, b = km, c = kn
            (ie) (Constant)
            (or) 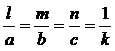(Constant)
To find direction cosines if direction ratios are given
            If a, b, c are the direction ratios then direction cosines are
           l  =
             similarly       m =                                                    (1)
                                n =
l2+m2+n2 =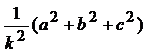
(ie)       1 =
           
Taking square root on both sides
            K =
            \

Problem
1. Find the direction cosines of the line joining the point (2,3,6) & the origin.
Solution
By the distance formula

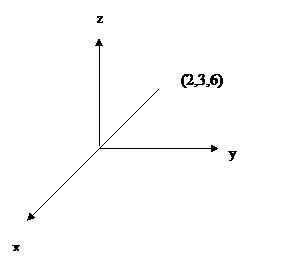
Direction Cosines are                                                                     r                                                                                                       
l = cos µ =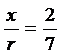                                                               

  m = cos b =                                                                 
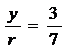
n = cos g =
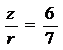
2. Direction ratios of a line are 3,4,12. Find direction cosines
Solution
            Direction ratios are 3,4,12
                (ie) a = 3, b = 4, c = 12
            Direction cosines are
                        l =
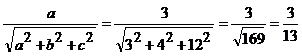
                    m=
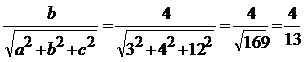
n=       
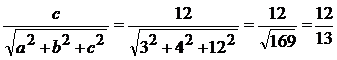
Note

• The direction ratios of the line joining the two points A(x1, y1, z1) &
  B (x2, y2, z2) are (x2 – x1, y2 – y1, z2 – z1)
• The direction cosines of the line joining two points A (x1, y1, z1) &

      B (x2, y2, z2) are
r = distance between AB.

Download this lecture as PDF here

`